SiamRCR: Reciprocal Classification and Regression for Visual Object Tracking

本文解决的是老生常谈的分类和回归不匹配的问题。作者提出在分类和回归之间建立双向的连接,可以动态地重新加权每个正样本的损失。此外,增加了一个定位分支用于预测定位精度,可以在推理过程中替代回归辅助连接(regression assistance link),使得训练和测试更加一致。最终运行速度为65FPS。
Introduction

首先点出问题,即孪生跟踪架构中分类和回归是分开独立优化的,导致二者不匹配。如图1所示,分类得分最高的位置生成的预测框不一定是最好的,或者预测比较好的框分类得分很低。这个图和IOUNet中的图很相似,事实上,这个问题在检测任务中已经被很多学者研究,并且有些成果也被应用到跟踪中。比如SiamFC++借鉴FCOS架构增加了一个衡量定位精度的分支,ATOM/DiMP系列使用IOUNet进行回归。作者指出这些方法仍然存在不匹配,因为并没有解决分类和回归独立优化的问题。
因此,本文提出在分类和回归之间建立一个互惠关系 (reciprocal relationship),使它们同步优化,以生成精度一致的输出。整体框架如图2所示,在分类和回归分支之间增加了两个连接 classification / regression assistance link。classification assistance 用分类置信度给回归损失加权,使得回归可以更关注高置信度的位置;regression assistance 用定位精度(预测框和gt的IOU)给分类损失加权,迫使分类分数与回归精度更加一致。
而在推理阶段,gt是未知的,无法通过计算IOU得到定位精度,因此额外增加一个定位分支专门用于预测定位精度。将分类置信度与定位预测置信度相乘,在推理阶段生成新的跟踪评分/置信度图,保证了与训练过程的一致性(类似FCOS / SiamFC++)。

Method
Overview
图2整体是一个anchor-free的孪生框架,预测头部分采用的是CenterNet的中心、中心偏移量、宽高的形式。这里将中心偏移量和宽高放在同一个分支输出,所以回归分支输出维度是4 $t^_{x,y} = (w^, h^, \Delta x^, \Delta y^*)$ 。
Reciprocal Classification and Regression
下面开始介绍两种辅助连接,设计原则就是:
- 当回归框的定位精度较低时,相应的分类得分不应该很高,因为如果该位置成为分类置信度的赢家,差的回归结果将导致跟踪性能较差;
- 当回归框的分类分数较低时,提高其定位精度是没有意义的,因为这个框一定不会是最后的输出。
Regression Assistance Link 针对准则1,将回归分支生成的框与gt计算IOU,看成一种动态的样本重加权作用于分类损失:
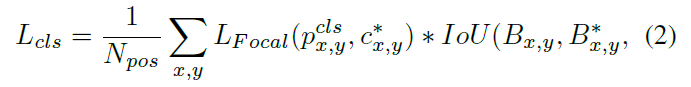
$N_{pos}$表示正样本个数,$B,B^*$分别表示预测框和gt。
Classification Assistance Link 针对准则2,将分类置信度 $p^{cls}_{x,y}$ 动态地重新加权回归损失:

Localization Score Branch 在训练时,regression assistance link使得分类分支考虑了回归精度,但这需要借助gt。而在推理阶段没有gt,为了保证训练和推理的一致性,使得推理阶段的分类分支也能考虑定位精度,作者额外增加了一个定位分支专门用于预测定位精度,作用类似FCOS / SiamFC++的centerness。其训练损失就是计算定位分支输出与IOU之间的交叉熵损失。

推理阶段示意图如图3,将分类分支和定位分支的得分相乘生成最后的跟踪分数图。

Experiments
Ablation Study

表1中这两个组件的性能提升几乎是正交的,联合使用的提升(5.05%)几乎等于单独使用时各自性能提升的和(3.54%+2.86%)。

图4展示了不同方法的跟踪分数和回归框IOU之间的相关性,(a)是baseline,(b)是centerness,(c)是basline+定位分支,(d)是SiamRCR。其中(b)和(c)类似,区别是分别使用IOU和centerness来衡量定位精度。
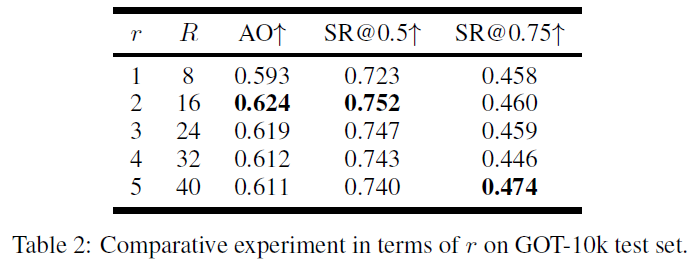
最后展示了划分正负样本时不同半径对结果的影响。
Comparison with the State-of-the-Art




小结
本文解决了孪生跟踪框架中分类和回归不一致的问题。印象中最先研究这个问题的是检测领域的PISA (Prime Sample Attention in Object Detection),根据IOU对样本进行排序然后选择prime sample。之后也有许多相关文章,包括本文的Regression Assistance Link也能看到一些检测里面的影子(吐槽一下我19年投了一篇文章有个点和这个一毛一样然而到现在都还没中hhh)。但目前的研究其实基本上都是在用回归矫正分类,而本文做了一个双向的矫正,(显式地)增加了用分类矫正回归的过程(为什么说是显式,因为其实只要把分类和回归乘到一起,这个作用就是相互的,比如公式2中,我可以把focal loss当成权重,IOU当成优化变量,那就变成了分类矫正回归)。这种显式的矫正似乎监督能力更强,如果有个消融实验对比一下单独使用公式3和公式4的效果就更直观了。