Learn to Match: Automatic Matching Network Design for Visual Tracking

Motivation
本文聚焦于孪生跟踪算法的匹配过程,目前主流的互相关操作是启发式设计的,严重依赖人工经验,并且单一的匹配方法无法适应各种复杂的跟踪场景。因此,本文引入了6种新的匹配算子来替代互相关。通过分析这些算子在不同跟踪挑战场景下的适应性,作者发现可以将它们结合起来进行互补,并借鉴NAS思想提出一种搜索方法 binary channel manipulation (BCM) 探索这些匹配算子的最优组合。
Analysis of Matching Operators
首先介绍本文采用的6种匹配算子,Concatenation, Pointwise-Addition , Pairwise-Relation , FiLM , Simple-Transformer 和Transductive-Guidance。

Concatenation 图2(a),将模板特征$F_z$ pool成 $f_z \in 1 \times 1 \times C$,再与搜索特征$F_x$拼接。

Pointwise-Addition 图2(b),将上面的拼接换成了对应元素相加。

Pairwise-Relation 图2(c),类似non-local,将$F_x, F_z$分别reshape成 $H_x W_x \times C$ 和 $C \times H_z W_z $,然后做矩阵乘法。相当于将模板中的每个元素都与搜索特征的所有元素衡量相似性。
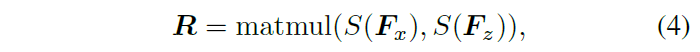
FiLM 图2(d),这个思路源于视觉推理,通过对神经网络的“中间特征”应用仿射变换来自适应地影响网络的输出。如公式5所示,对$f_Z$卷积变换后得到系数$\gamma$和偏置$\beta$,将其作用于搜索特征$F_x$


Simple-Transformer 图3(a),就是multi head attention。
Transductive-Guidance 图3(b),源于VOS中的掩码传播机制,即用前一帧的掩码引导当前帧的预测。首先像Pairwise-Relation一样计算模板和搜索特征之间的对应关系(affinity)(公式7),然后用第一帧的伪掩码进行调制(公式8),生成的$G$中的每个位置表示前景的概率,最后将$G$与原始搜索特征$F_x$相加(公式9)。整个过程可以参考该作者另一篇文章OceanPlus。

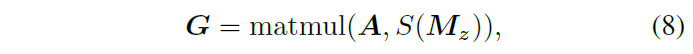

Analysis
作者将上述6种算子与传统的互相关匹配分别在OTB100上进行测试,比较其性能,如表1所示。
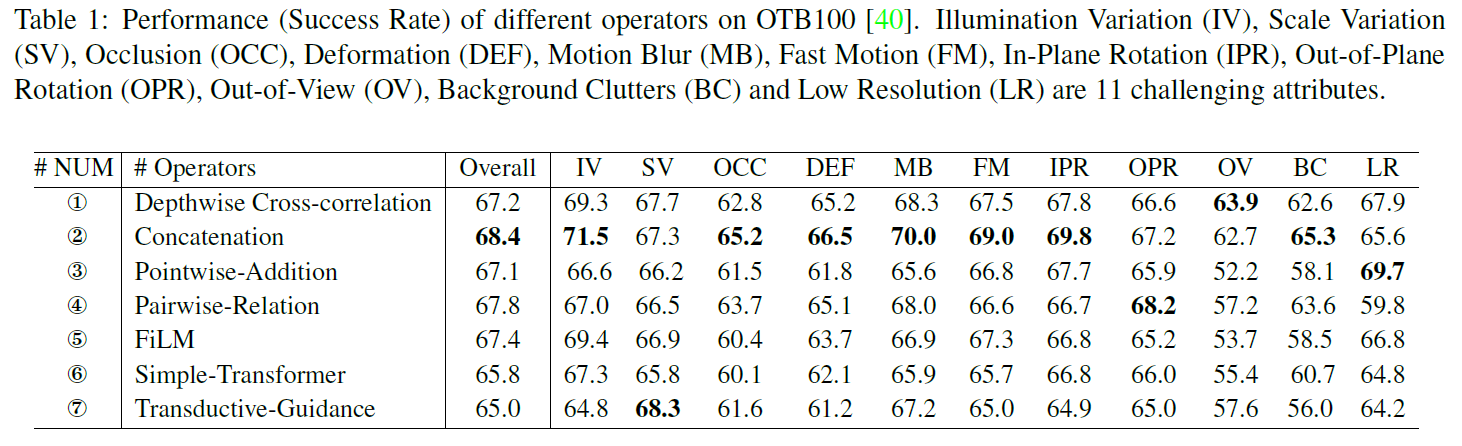
对于单一的匹配算子,除了6和7,其他的均取得了和dw-corr相当的性能,甚至2(直接拼接)的性能更好。
虽然2的性能最优,但并不能保证其在所有跟踪挑战中都是最好的,比如在SV,OPR,OV和LR上就被其他算子超过。作者在图4进一步可视化了响应图,可以看到depthwise cross-correlation (a), Pairwise-relation (d), and Transductive-Guidance (g)更关注目标本身;而the concatenation (b), Pointwise-Addition (c), Simple-Transformer (e), and FiLM (e)则包含了更多上下文信息。

上述结果表明不同的匹配算子在不同跟踪场景下具有不同的可靠性,由此想到是否可以将它们结合起来,利用这些特征进行互补。因此,作者接下来提出一种自适应学习的自动选择和组合匹配算子的方法。
Methodology

图5为整体框架,首先将模板和搜索特征送入多个匹配算子构成的搜索空间,生成m个响应特征 $\{ r_1, r_2, … , r_m \}$,给每个响应特征的每个通道都赋予一个可学习的调制器(manipulator) $\omega_i^j$,表示该通道的贡献。然后引入二元Gumbel-Softmax来离散化这些调制器进行二元决策,训练过程参考DARTS的两层优化。最后根据学好的调制器保留两个匹配算子构建新的跟踪器再次训练。
下面分别介绍二元的通道调制器(Binary Channel Manipulation)和两层优化(Bilevel Optimization)
Binary Channel Manipulation
Binary Channel Manipulation (BCM) 用于决定匹配算子对目标状态预测的贡献,它给每个匹配响应特征的每个通道都赋予一个可学习的调制器(manipulator) $\omega_i^j$,将所有调制后的特征拼接聚合成一个大的特征(有点类似NAS里的supernet)。

其中$r_i^j$ 表示第 i 个响应特征的第 j 个通道。对于每个匹配算子,我们将其对应的所有通道调制器相加得到该算子的potential $p_i$,这个在后面选择匹配算子时会用到。
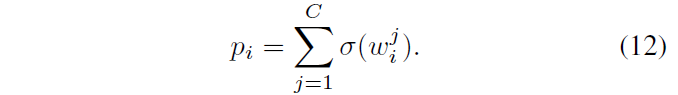
接下来,将连续的$\omega_i^j$转换为离散的,离散后的类别是二值分类,概率向量为$\pi = \{ \pi_1 = \sigma(\omega_i^j), \pi_2 = 1 - \sigma(\omega_i^j) \}$。为了能够可微的反向传播,这里利用Gumbel-Softmax进行训练。对概率向量$\pi$对应的随机变量添加Gumbel噪声$g_k$后随机采样

然后将argmax替换为Softmax定义一个连续可微的近似

因为这只是一个二值概率分布,公式14带入$\pi$的表达式后可以被简化成

推导如下:

作者这里令$\tau=1, g_k=0$,对于离散采样的样本d,前向传播时使用硬值(0或1),反向传播采用软值获得梯度。

Bilevel Optimization
优化的目标有两部分,一个是调制器参数$\omega$,另一个是匹配网络的卷积层参数$\theta$。这里借鉴DARTS的优化方法,利用训练集优化$\theta$,利用验证集优化$\omega$,记作
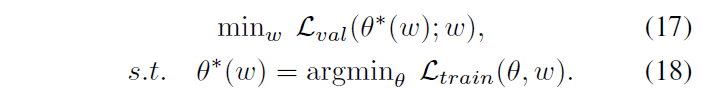
为了加速收敛,将其简化成

按上述方式训练后,保留potential $p_i$最高的两个匹配算子构成新的跟踪器重新训练。
Experiments
Implementation Details
训练过程分成匹配网络的搜索和新跟踪器的训练两个阶段,第一阶段用Bilevel Optimization搜索最优的匹配网络组合,第二阶段用优化的匹配网络构建一个新的跟踪器进行常规的训练。搜索算法为分类和回归分支确定不同的匹配网络。经过第一阶段的训练后,分类分支使用Simple-Transformer和FiLM,而回归分支使用FiLM 和 Pairwise-Relation。
State-of-the-art Comparison


Ablation and Analysis
One or Many Manipulators 本文给匹配算子的每个通道都赋予一个调制器,作者也尝试了给每个匹配算子只赋予一个标量的调制器,性能会有所下降 OTB100 69.5,LaSOT 54.7。
Random Search 随机选择匹配算子同样会使性能下降,OTB100 69.1,LaSOT 53.2。
NAS-like Matching Cell 用DARTS的方法构建一个有向无环图进行搜索,如图7所示,同样不如本文的结果,且速度会大幅下降。

Conclusion
- DW-Corr并不是孪生跟踪算法的最优选择,本文设计了6种新的匹配算子;
- 本文用一种自动搜索的方式组合出最优的匹配网络。