Saliency-Associated Object Tracking

Motivation
和上一篇一样是研究跟踪的匹配问题。目前主流的跟踪策略分为全局和局部两种,全局策略(如DW-Corr)学习目标的整体表示,当目标发生较大变化时表现不佳。局部策略(如PG-Corr)将目标分割成多个patch,并行跟踪所有patch,通过聚合这些patch的跟踪结果,推断出目标状态。而局部策略的局限在于并不是所有patch都包含丰富的信息,一些没有判别能力的patch难以跟踪,可能对推断目标状态产生不利影响。因此,本文提出只跟踪目标的显著局部区域而不是简单跟踪所有局部块,具体提出了细粒度的显著性挖掘模块(fine-grained saliency mining module),用于捕获局部显著性;以及显著性关联模块(saliency-association modeling module) 将捕获的显著区域关联在一起,学习目标模板与搜索图像之间的全局相关性,以进行状态估计。
Method
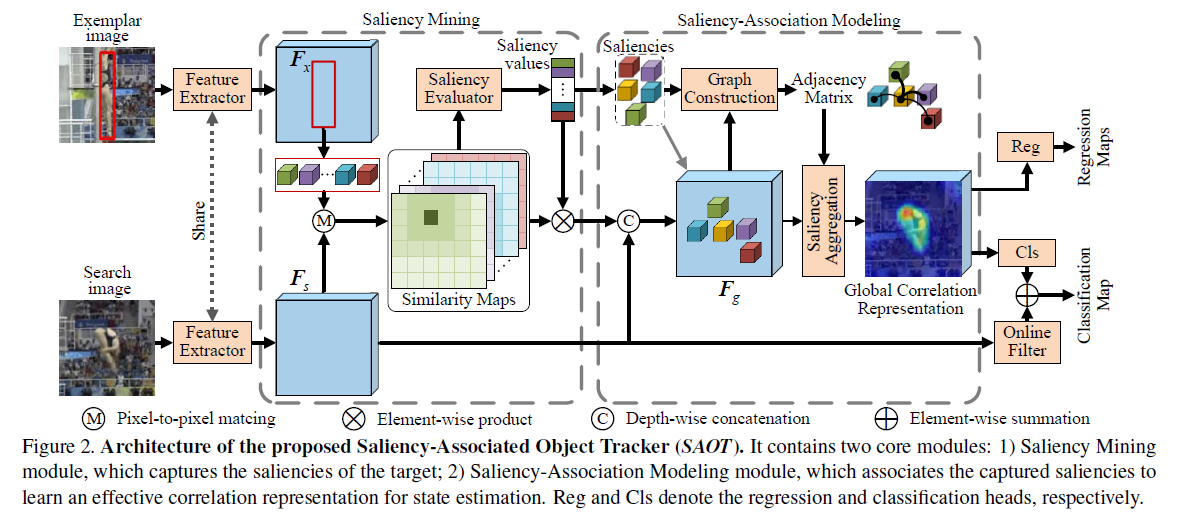
Overall Framework
整体框架如图2所示,模板特征$F_x \in \mathbb{R}^{h_x \times w_x \times c } $ 和搜索特征 $F_s \in \mathbb{R}^{h_s \times w_s \times c } $ 首先送入Saliency Mining module用于提取模板的局部显著性,该模块计算模板和搜索特征的pixel-to-pixel相似性,选择局部最大且最锐利的点(local sharp maximum points) 作为显著点,这些显著点表示模板中最具判别性的区域。
然后,Saliency-Association Modeling module将捕获的显著点进行关联,以学习模板和搜索图像之间的有效全局相关性表示。最后再对相关性结果进行状态估计。
Saliency Mining
显著性挖掘模块用于捕获模板中具有判别能力的局部显著区域,包括两个步骤:
- 为模板$F_x$中的每个点构建与搜索特征$F_s$的相似图;
- 根据相似图衡量$F_x$中每个点的显著性,从而进行选择。
Construction of similarity maps
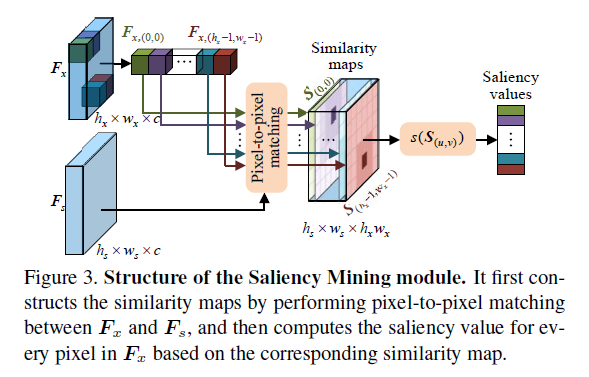
pixel-to-pixel相似图的构建如图3所示,将模板特征中的每个点$(u,v)$与搜索特征计算余弦距离,得到单通道的相似图$S_(u,v) \in \mathbb{R}^{h_s \times w_s}$,总共会生成$h_x \times w_x$这样的相似图。
Saliency evaluation 接下来根据每个相似性图中最大值点附近的峰值分布(包括强度和集中度)来评估对应模板特征点的显著性。强度使用峰值旁瓣比PSR进行衡量
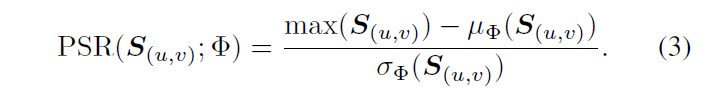
其中,$\Phi$表示旁瓣,$\mu_{\Phi}, \sigma_{\Phi}$分别表示旁瓣的均值和方差。在原始的PSR中,主瓣$\Psi$的大小是预定义的固定值,作者认为这样定义是不合理的,因为没有考虑响应图的分布。图4展示了两种不同峰分布的相似图,这两个相似图显然对应着主瓣的大小不同。
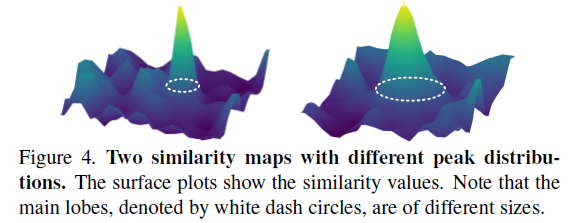
为了消除这一影响,作者将主瓣的边界定义为峰附近最靠近的轮廓,其高度等于整个相似图的平均值。至此,我们可以得到相似图$S_{ (u,v) }$的峰强度$\gamma$:
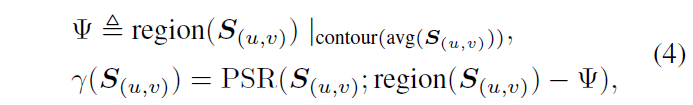
用于显著性评价的另一个度量是峰分布的集中度(concentration),它与主瓣覆盖面积$A_{\Psi}$成反比。
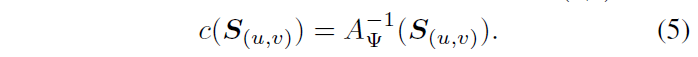
将上面的强度和集中度结合起来就得到了相似图$S_{ (u,v) }$的显著性$s( S_{ (u,v) } )$:
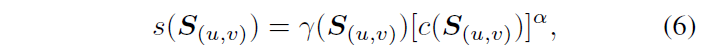
考虑到应该尽可能跟踪目标模板的中心,因此在计算显著性时额外增加一个高斯正则项,公式7中的高斯项$g$是与模板中心对齐的。
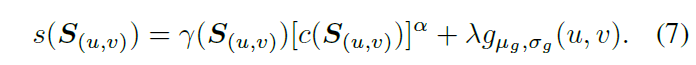
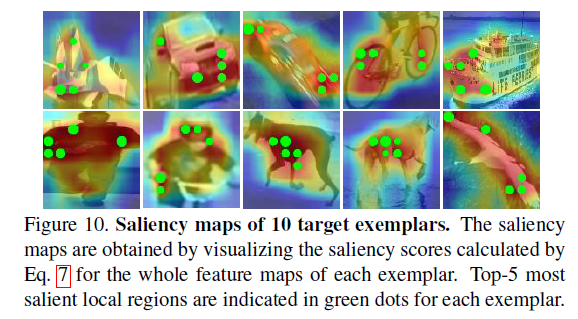
根据公式7的显著性评价方式,我们可以计算模板特征$F_x$中每个点的显著性,并选取K个最大的点构成显著性集合 $P_x = \{ p_x^k \}_{k=1}^K$,这个显著性结合在搜索特征$F_s$的对应匹配点集合为$P_s = \{ p_s^k \}_{k=1}^K$。
Saliency-Association Modeling
显著性关联模块利用捕获的显著性来学习模板和搜索特征之间的全局关联,作者利用图的方式进行构建,同样包括两步:
- 在捕获的显著性之间构建一个图,以建模这些显著性之间的交互关系;
- 基于构造的图聚合显著性。
Construction of the saliency graph 构建显著性图时同时考虑了相似图$S$和搜索特征$F_s$,将二者拼接得到 $F_g$,共有$h_s \times w_s$ 个节点,每个节点的维度是 $h_x w_x + c$。然后构建图的边,如图5所示,包括两种类型,一种是对显著点之间进行连接,另一种是对每个点和其邻域点进行连接,边的集合定义为$C$。
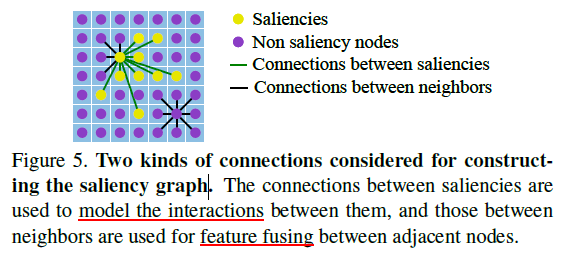
本文用两层全连接层来学习边的权重,定义权重的邻接矩阵为 $A \in \mathbb{R}^{N \times N}, N=h_s w_s $
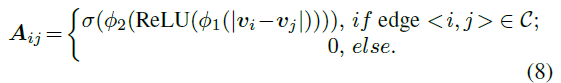
其中 $v1, v2$是图的两个节点,$\phi_1, \phi_2$是两层全连接层,用sigmoid函数约束权值范围在0到1之间。只有当边$\langle i, j \rangle$符合图5中的两种情况才有权值。
Aggregation of the captured saliencies 使用两层的GCN进行显著性聚合
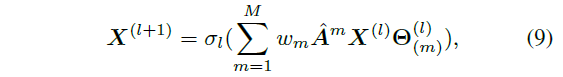
其中m和M表示多项式的阶数和总阶数,$\omega_m$是可学习权重。$\hat{A} = \tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{\frac{1}{2}}$是normalized邻接矩阵,$\tilde{A}=A+I$,$ \tilde{D}$是$\tilde{A}$的对角阵,这些均为图卷积知识。$X^{l} \in \mathbb{R}^{N \times d_l}$和$X^{l+1} \in \mathbb{R}^{N \times d_{l+1} }$是第 l 层上所有节点的输入和输出特征,其中 $d_l, d_{l+1}$是对应的特征维度,$d_0 = h_x w_x + c$,$ \Theta_m^l \in \mathbb{R}^{d_l \times d_{l+1}} $是第l层第m阶的参数矩阵。
通过构造显著性图并进一步进行显著性聚合,Saliency-Association Modeling module能够学习目标模板与搜索图像之间的全局相关表示,进而用于预测搜索图像中的目标状态。
Tracking Framework
跟踪框架如图2所示,预测头采用FCOS,并增加DiMP的在线跟踪。
Experiments
Ablation Study
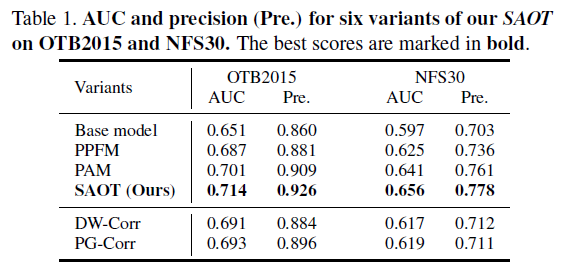
Base model 只有特征提取,DiMP的在线分类,以及预测头;
PPFM 只做图3的Pixel-to-Pixel匹配,然后将拼接后的$S$和$F_s$直接过两层卷积得到相关结果;
PAM 没有提取显著性,将所有局部平等的进行关联(类似self-attention);
PPFM和base model的对比证明建模模板和搜索图像之间的相似性是有益的,PAM和PPFM的对比证明将匹配的局部进行关联是有益的;最后SAOT和PAM的对比证明了局部显著性是有益的。最后还与经典的DW-Corr和PG-Corr进行比较。
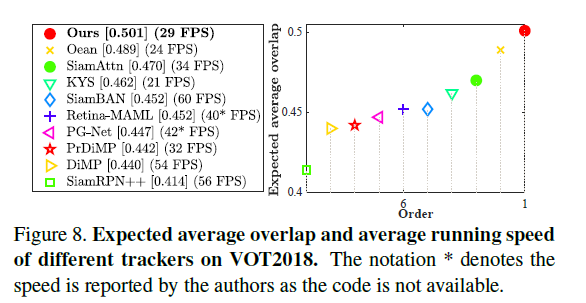
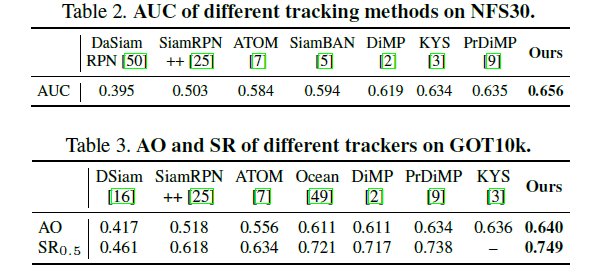
SOTA Comparison
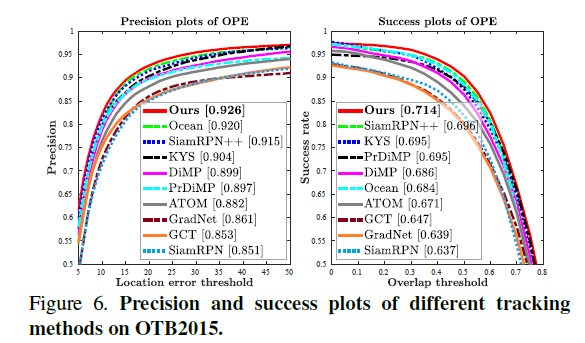
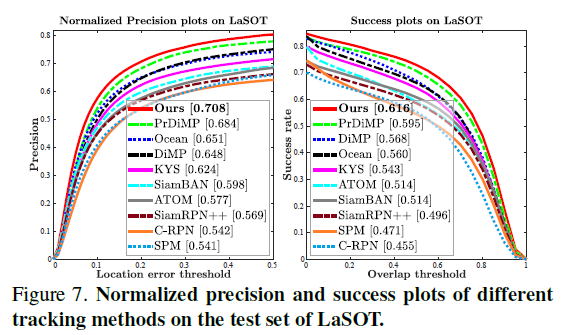
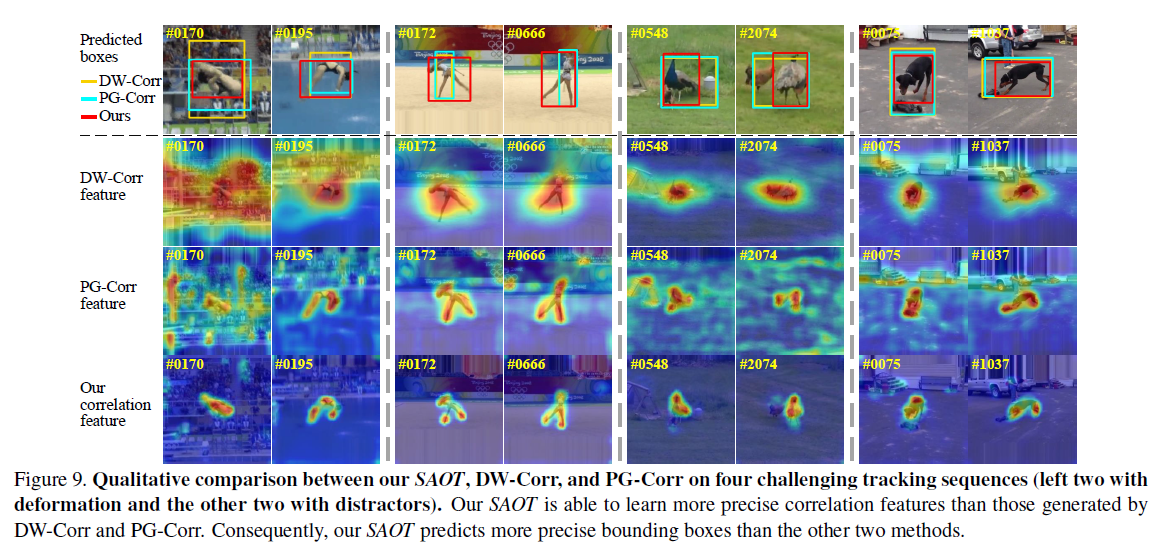
Qualitative Study
可视化结果有点牛逼,对于形变和干扰场景的响应看上去非常好。