RPT++: Customized Feature Representation for Siamese Visual Tracking
Motivation
本文是去年RPT方法的改进,作者来自同一团队。出发点是现有的跟踪方法对于分类和回归使用的是同一套特征,而作者指出这两个任务是有差异的,因此对特征的需求也是不同的。如图1所示,分类需要的是显著区域中更具有判别力的特征,而回归需要边界附近的特征来精确定位。针对这一问题,作者提出了两种定制化的特征提取,用于捕获特定任务的视觉模式。其中Polar Pooling从语义关键点收集丰富的信息,以进行更强的分类;而Extreme Pooling捕获目标边界的清晰视觉模式,实现目标状态的精确估计。

Introduction
首先分析一下现有pipeline的局限。主流的anchor和anchor-free的方法都是在一个特征点上进行分类和回归,这种基于点的特征表示方法传递显式语义和边界信息的能力较弱。另一些方法通过提取目标框内的ROI特征来提升表征目标的能力,但矩形框可能包含多余的背景像素,且缺乏对物体几何结构的建模能力。
为了解决这些问题,作者先cue了一下之前的工作RPT。RPT用若干个有代表性的点集来表示目标,通过可变形卷积自动学习语义显著性和边界区域的特征。这种方法比单点特征包含更多可识别的信息,有助于真正理解对象的视觉模式。但是,RPT提取的关键点真的都可靠吗?事实上,RPT经常提取一些位于背景显著区域的错误关键点。 并且RPT用于分类和回归的特征均取自相同的点集,忽略了这两个任务之间的不对齐。如上面图1介绍的,从语义关键点提取的特征为分类提供了更具判别力的视觉模式,而边界附近的特征编码了关于空间范围的先验知识,有助于准确估计目标状态。这两个任务在特征表示中的差异极大地限制了跟踪器的性能。
因此,本文在RPT的基础上定制了两个特征提取器,分别从对应的关键点中获得语义显著信息和边界极值信息。其中,Polar Pooling通过计算从中心到每个语义关键点的径向最大响应来捕获目标区域内更精确的视觉模式。Extreme Pooling通过一个额外的不确定性分支来消除边界极值点估计中的模糊性。最后将这两个增强后的特征分别送入分类和回归分支。
Method
Baseline
首先回顾一下baseline的RPT方法。在模板和搜索特征做互相关后,相关图上的每个特征都可以看成一个目标候选,用一系列代表性点集表示。

其中n表示点的个数,默认为9个。RPT通过两步来细化这些点的分布:

公式2可以通过下图直观理解,对于一个初始中心点$(x_k, y_k)$,先通过回归偏移$\{(x_k^c, y_k^c)\}^n_{k=1}$得到一个粗略的点集,然后对每个点再进行一次微调$\{(x_k^r, y_k^r)\}^n_{k=1}$得到最终的目标状态。RPT通过可变形卷积得到更强大的特征表示,能够对物体的几何变换进行建模,生成的特征同时用于分类和回归。而下面介绍的改进就是通过两个不同的模块生成不同的特征进行分类和回归。

Framework of RPT++

RPT++整体框架如图2所示,首先预测相关特征图上每个位置的粗略关键点集,包括四个边界极值关键点(左上右下)和五个语义关键点。将四个边界点转换为伪框如下:
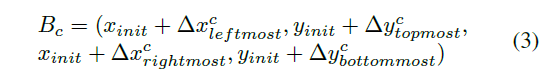
其中$(x_{init}, y_{init})$表示相关特征图上每个点,$\Delta x^c_{leftmost}, \Delta x^c_{topmost}, \Delta x^c_{rightmost}, \Delta x^c_{bottommost}$对应左、上、右、下的极值关键点的伪框偏移量。与RPT不同的是,本文还额外估计了每个偏移量的不确定性,用一个高斯分布表示。

其中均值$o_e \in \{ \Delta x^c_{leftmost}, \Delta x^c_{topmost}, \Delta x^c_{rightmost}, \Delta x^c_{bottommost}\}$表示预测偏移量,方差$\sigma$表示不确定性。这种方法常用于目标检测中,用一个概率分布来表示回归预测而不是仅仅估计一个硬值,从而预测回归的不确定性。
总结一下,粗略关键点集的预测对相关特征图上的每个位置,在回归分支输出n个2D偏移量,以逐点的方式细化样本点的分布;在不确定性分支输出4个伪框偏移量的不确定性。接下来,我们将语义关键点送入polar pooling得到更利于分类的视觉表示,将边界极值关键点和不确定性预测送入extreme pooling得到更精确的边界框。
Customized Feature Extraction
Extreme Pooling 在某些情况下,目标的极值点是不明确的(例如,沿着车辆边界顶部的任何一点都可能被视为极值点)。这些模糊性使得有效的极值特征难以提取,直接限制了定位精度。Extreme pooling就是为了解决这一问题,具体来说,既然我们已经得到了每个边界极值点的不确定性,那么提取边界特征时就不用局限仅提取该点的特征,而是可以提取该点附近的一个不确定性区域的特征,这样可以更好地描述目标边界。整个过程如图3所示。

Extreme pooling首先在每个边界极值点$(x_e,y_e)$上根据其对应的不确定性$\sigma$裁剪一个区域

其中$(x_1,y_1), (x_2,y_2)$表示裁剪区域的角点,$\mu$是缩放因子,这个不确定性区域的大小为$2\mu\sigma \times 2\mu\sigma \times C$。然后将该区域的特征送入ROIAlign+MaxPool,还原成$1 \times 1$的特征。将4个极值点都做一样的操作并与原始特征拼接,就得到了通道维度为5C的特征,其中包含了边界的不确定性。
Polar Pooling 伪框中的语义关键点经常落在目标之外的背景上,这传达了不准确的视觉模式。因此作者设计了polar pooling,如图4所示。

将原始点到每个语义关键点的径向路径平均分为N个点,取这N个点的最大值特征作为输出,用公式7表示。

其中$(x_c,y_c), (x_s,y_s)$分别表示原始点和语义点的坐标,括号里的坐标可能是小数,采用双线性插值进行估计。最后,将5个语义点的输出特征值$F_s$与原始特征拼接起来,构造语义增强的特征,通道维度为6C。
Loss Function
损失函数包括三部分
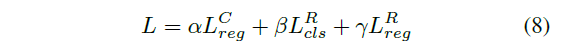

其中$L_{reg}^C$表示学习粗略点集的KL loss,参考这篇博客;$L_{cls}^R, L_{reg}^R$是refine过程中的Focal loss和IOU loss。
Experiments
Comparison with SOTA



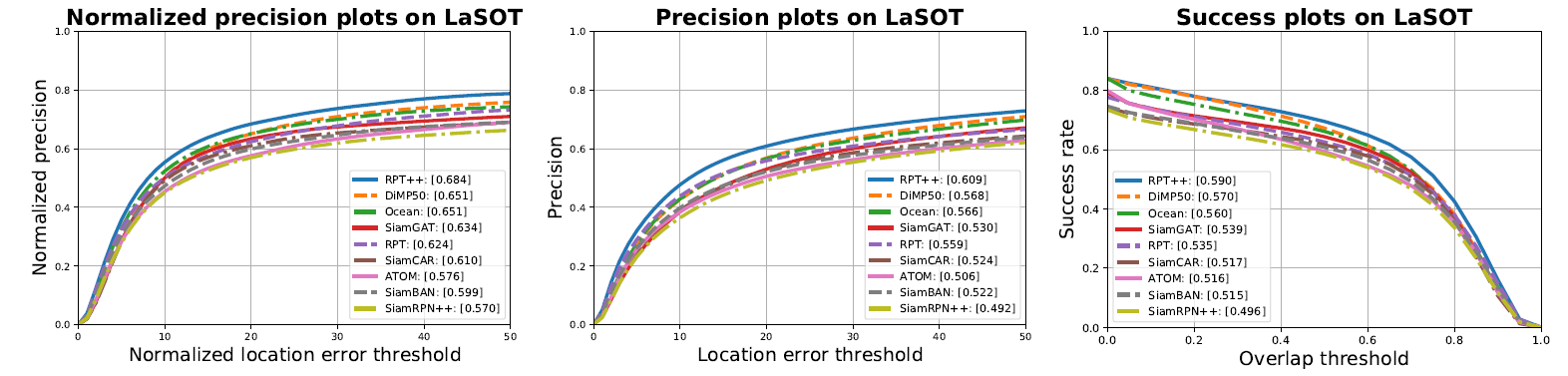
Ablation Study

表5 RPT++各个组件的消融实验
表6 polar pooling径向采样个数N分析
表7 extreme pooling缩放因子$\mu$ 分析
表8 extreme pooling 采样窗口的影响,对比了固定大小的crop以及根据不确定性crop。
